今天来聊聊关于已知p是边长为2的正六边形abcdef内的一点,如图1正六边形ABCDEF的边长为aP是BC边上一动点过P作PM的文章,现在就为大家来简单介绍下已知p是边长为2的正六边形abcdef内的一点,如图1正六边形ABCDEF的边长为aP是BC边上一动点过P作PM,希望对各位小伙伴们有所帮助。
1、(1)①60°,②证明见解析;(2)证明见解析;(3)四边形MONG是菱形,理由见解析. 试题分析:(1)①运用∠MPN=180°-∠BPM-∠NPC求解。
2、②作AG⊥MP交MP于点G,BH⊥MP于点H,CL⊥PN于点L。
 (相关资料图)
(相关资料图)
3、DK⊥PN于点K,利用MP+PN=MG+GH+HP+PL+LK+KN求解,(2)连接OE。
4、由△OMA≌△ONE证明,(3)连接OE,由△OMA≌△ONE。
5、再证出△GOE≌△NOD,由△ONG是等边三角形和△MOG是等边三角形求出四边形MONG是菱形.试题解析:(1)①∵四边形ABCDEF是正六边形,∴∠A=∠B=∠C=∠D=∠E=∠F=120°.又∴PM∥AB。
6、PN∥CD,∴∠BPM=60°,∠NPC=60°。
7、∴∠MPN=180°-∠BPM-∠NPC=180°-60°-60°=60°,故答案为;60°.②如图1,作AG⊥MP交MP于点G。
8、BH⊥MP于点H,CL⊥PN于点L,DK⊥PN于点K。
9、MP+PN=MG+GH+HP+PL+LK+KN.∵正六边形ABCDEF中,PM∥AB,作PN∥CD。
10、∵∠AMG=∠BPH=∠CPL=∠DNK=60°,∴ ,∵AM=BP。
11、PC=DN,∴MG+HP+PL+KN=a,GH=LK=a。
12、∴MP+PN=MG+GH+HP+PL+LK+KN=3a. (2)如图2,连接OE,∵四边形ABCDEF是正六边形。
13、AB∥MP,PN∥DC,∴AM=BP=EN。
14、又∵∠MAO=∠NOE=60°,OA=OE,在△ONE和△OMA中。
15、 ,∴△OMA≌△ONE(SAS),∴OM=ON.(3)如图3。
16、连接OE,由(2)得,△OMA≌△ONE。
17、∴∠MOA=∠EON,∵EF∥AO,AF∥OE。
18、∴四边形AOEF是平行四边形,∴∠AFE=∠AOE=120°,∴∠MON=120°。
19、∴∠GON=60°,∵∠GON=60°-∠EON,∠DON=60°-∠EON。
20、∴∠GOE=∠DON,∵OD=OE,∠ODN=∠OEG。
21、在△GOE和∠DON中, ,∴△GOE≌△NOD(ASA)。
22、∴ON=OG,又∵∠GON=60°,∴△ONG是等边三角形。
23、∴ON=NG,又∵OM=ON,∠MOG=60°。
24、∴△MOG是等边三角形,∴MG=GO=MO,∴MO=ON=NG=MG。
25、∴四边形MONG是菱形.。
相信通过如图1正六边形ABCDEF的边长为aP是BC边上一动点过P作PM这篇文章能帮到你,在和好朋友分享的时候,也欢迎感兴趣小伙伴们一起来探讨。
本文由用户上传,如有侵权请联系删除!






 广东省新一轮送教支教活动在西藏林芝市第三幼儿园举行
广东省新一轮送教支教活动在西藏林芝市第三幼儿园举行
 广东医谷:2022年“创客广东”生物医药专题赛圆满落幕
广东医谷:2022年“创客广东”生物医药专题赛圆满落幕
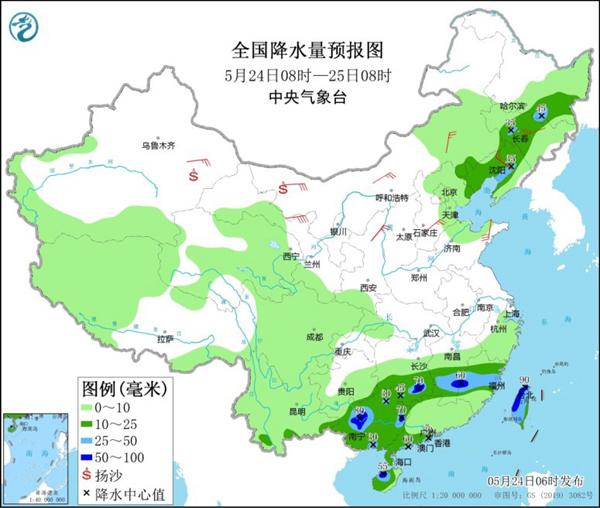
 南方频繁阴雨持续至月底 北方大范围降温
南方频繁阴雨持续至月底 北方大范围降温
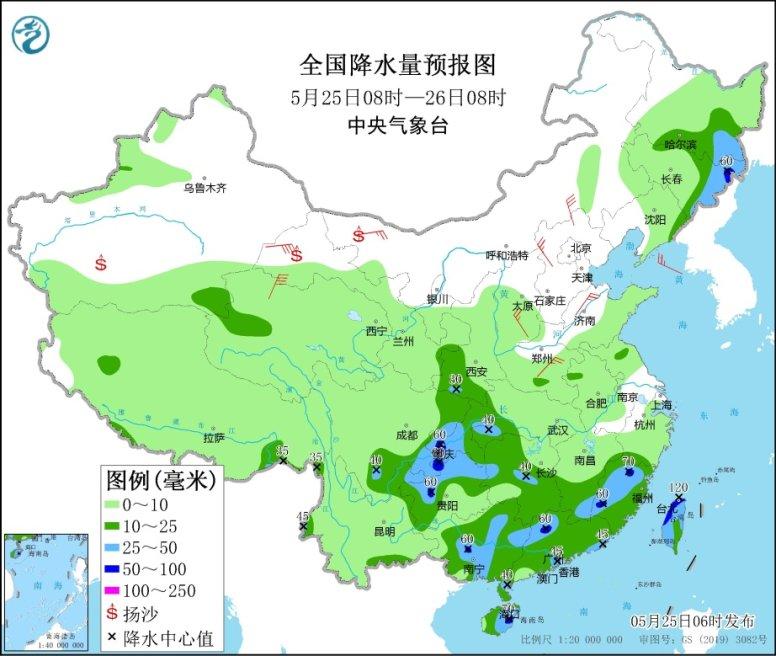
 东北黄淮等地有强对流天气 江南华南及贵州等地多降雨
东北黄淮等地有强对流天气 江南华南及贵州等地多降雨
 《只此青绿》被抄袭 舞蹈作品维权难在哪里?
《只此青绿》被抄袭 舞蹈作品维权难在哪里?
Copyright © 2015-2022 南方时尚网版权所有 备案号:粤ICP备18023326号-21 联系邮箱:855 729 8@qq.com